2013 IAGA Meeting

A Laboratory Planetary Core

Transport, Waves, and Magnetic Fields in Spherical Couette Flow at Very High Re.

Daniel S. Zimmerman
Santiago A. Triana
Daniel P. Lathrop
Work made possible by:
NSF/MRI EAR-0116129
NSF EAR-1114303
University of Maryland Physics/IREAP/Geology

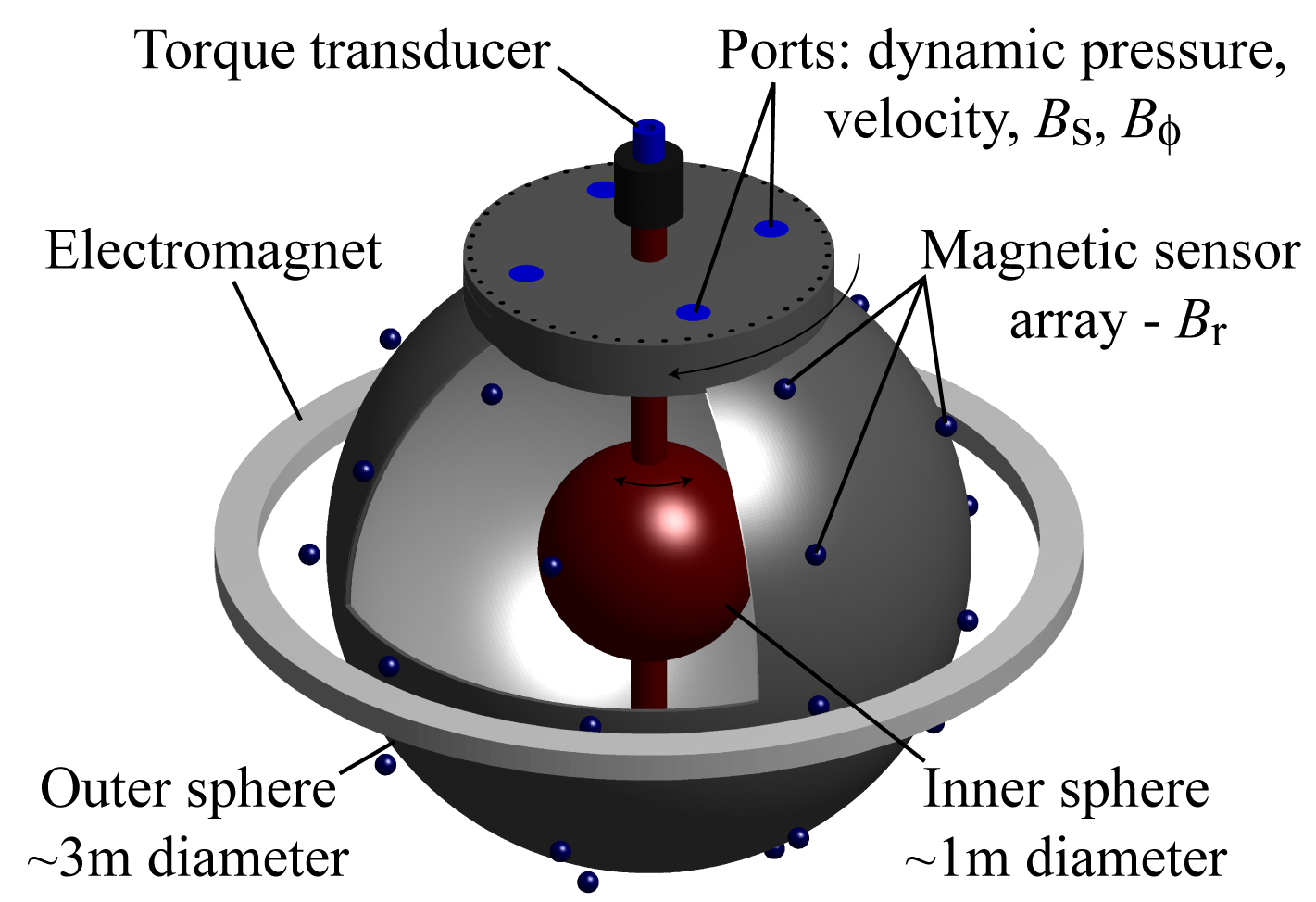
The Experiment

Stats:

Outer sphere maximum speed $$\Omega_o/2\pi=4\mathrm{Hz}$$
Inner sphere maximum speed $$\Omega_\mathrm{i}/2\pi=\pm20\mathrm{Hz}$$
Total rotating mass: 20 tons (18000kg)
- 7 ton (6300kg), 3m diameter shell
- 13 tons (12000kg) fluid (water, sodium metal)
Two 250kW (350HP) motors
Hot oil system: 120kW heating + 500kW cooling

Outer sphere at two revolutions/second

Why 13 Tons of Spinning Sodium?

Sodium best chance for liquid metal dynamo.
Fast rotation for self-organization.
Large and relatively slow rotating for "strong" magnetic effects.
Waves and other large-scale flows with low boundary friction.

Geometry & Forcing

Design:

Geometrically similar to Earth's core: $$\Gamma = r_\mathrm{i}/r_\mathrm{o} = 0.35$$
Imposed differential rotation (not convection!) to provide stirring in rotating frame.
Simple geometry: good for simulation
Common features with planetary core, not a scale model.

Instrumentation

Dimensionless Numbers

$$Ro = \frac{\Delta\Omega}{\Omega_o},0.01<|Ro|<100 $$
$$E = \frac{\nu}{\Omega_o(r_o-r_i)^2},10^{-8}< E<10^{-6}$$
$$Re = \frac{\Delta\Omega(r_o-r_i)^2}{\nu}, 10^6 < Re < 10^8 $$
$$Rm = \frac{\Delta\Omega(r_o-r_i)^2}{\eta}, 10 < Rm < 1000$$
$$Pm = \frac{\nu}{\eta} = \frac{Rm}{Re} \sim 10^{-5}$$
$$S = \frac{B_0 (r_o-r_i)}{\eta\sqrt{\rho \mu_0}}, 0 < S < 6 $$
$$\Lambda = \frac{B_0^2}{\rho\mu_0\eta\Omega_o},0 < \Lambda < 13\:\: (2\pi/\Omega_o = 30s)$$

Hydrodynamic Outline

Many turbulent flow states at different Ro.
Some flow transitions show large changes in angular momentum transport.
Turbulent scaling at fixed Ro.

Torque vs. Reynolds Number, Outer Stationary

Torque vs. Reynolds Number, Outer 1.25Hz

$$Ro = \Delta\Omega/\Omega_o$$

State Transitions: Torque and Azimuthal Velocity

$$\small Ro = 2.33$$

Phys. Fluids 23, 065104 (2011) - http://arxiv.org/abs/1107.5082

State Transitions: Mean Flows

Phys. Fluids 23, 065104 (2011) - http://arxiv.org/abs/1107.5082

State Transitions: Waves

Velocity frequency spectra:

Angular Momentum Transport: Torque vs. Ro

$$\small G(Ro,Re) = f(Ro)G_\infty(Re)$$

MHD Outline

Strong generation of B_φ (Ω-effect), large Ro-dependence, peaks at Ro=+6.
Strong applied field: new states, reduced Ω-effect, dipole moment enhancement from "dynamo-like" feedback loop.

Internal Field and External Gauss Coefficients

$$\scriptsize B_r(r,\theta,\phi,t) = \sum_{l=0}^{l=4}\sum_{m=0}^{m=l}l(l+1)\left(\frac{r_\mathrm{o}}{r}\right)^{l+2}P_l^m(\cos{\theta})(g_l^{m,s}(t)\sin{m\phi}+g_l^{m,c}(t)\cos{m\phi})$$
$$\scriptsize B_l^m = l(l+1)g_l^m$$

Internal Magnetic Field, "Weak" Applied Field

$$S=0.39$$Note: legend typo: circles are always B_φ

Internal Magnetic Field vs. Applied Field

State Changes at Strong Field

RMS Gauss Coefficients & Torque

Dipole Bursting State

$$\small S=3.5, Ro = +6, Rm = 430, E = 1.2\times10^{-7} $$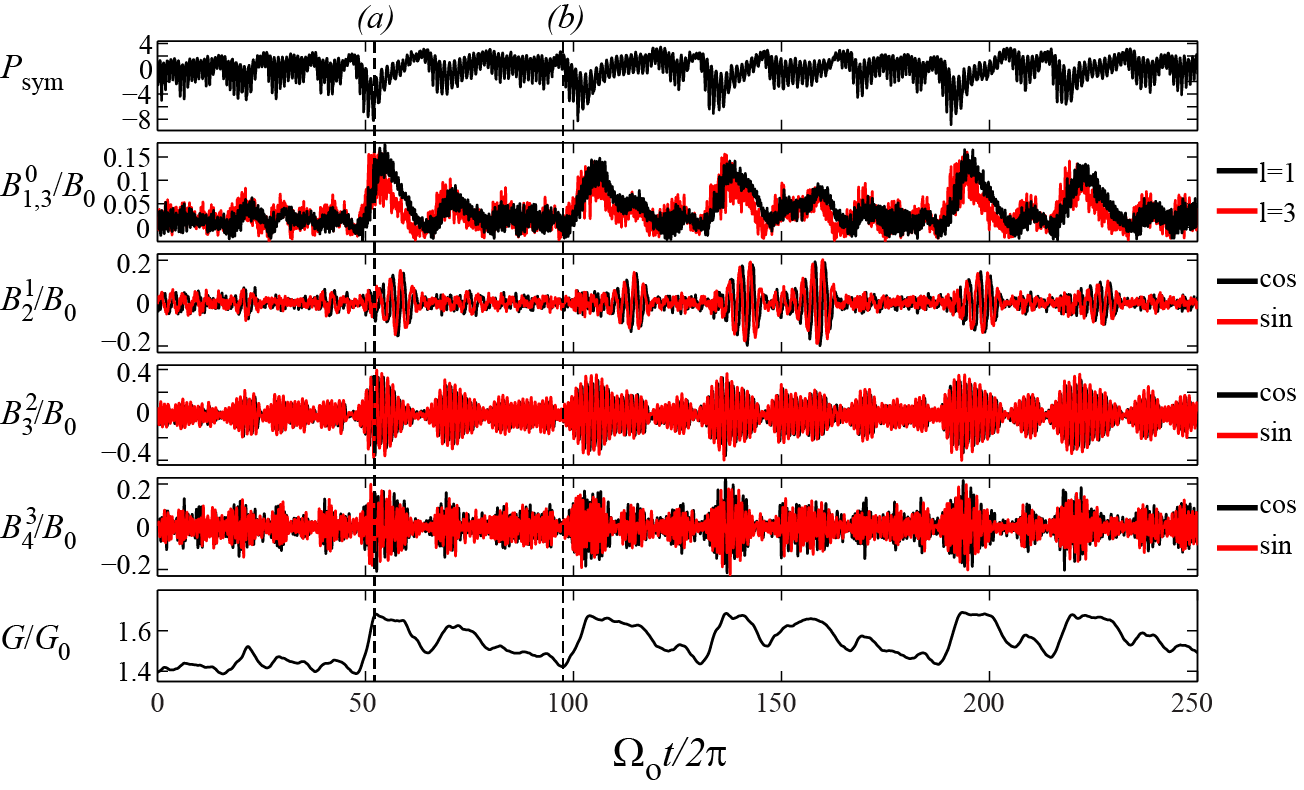

Ro=+6.0, S=3.5, Rm=430, E = 1.2x10^-7, Re = 5x10⁷
20% actual speed

Dynamo-style feedback?

Axisymmetric flow can't induce external dipole
from axisymmetric applied field.

Summary

Many different turbulent flow states in high-Re spherical Couette controlled by Ro.
Different turbulent states have much different large scales: mean flows and waves.
Large Ro-dependence of Ω-effect due to hydrodynamic state changes.
Strong applied field: new states, reduced Ω-effect, dipole bursts with a "dynamo-like" feedback loop.
Dipole enhanced by large scale nonaxisymmetric waves
Movie code: https://github.com/danzimmerman/matlabmag

Challenges and Promises

Data so far can provide good quantitative tests for models: Gauss coefficients, torque, waves, azimuthal and radial field.
To model spherical Couette for dynamo purposes, need to capture same states. Do we? Re high enough?