Background
The Jupyter notebook used to generate the content on this page optimizes the directivity of an arbitrary two-dimensional radio antenna array using M.T. Ma's algorithm presented in Chapter 3 of Theory and Application of Antenna Arrays. The directivity of an antenna is the ratio of power intercepted or radiated in a particular direction normalized by the three-dimensional average of the radiated power. The higher the directivity, the more the antenna can discriminate against signals from unwanted directions.
As of 8/9/2020 I refactored the optimal computation code into a class with a IPyWidget UI and made this
updated notebook with a easier-to-use UI. This leverages my n3ox_utils
package for a wire-entry interface.
This work was performed at the request of an acquaintance who was hoping to synthesize higher-performance arrays for long-wave radio reception on the amateur radio bands. Small (relatively) arrays of actively amplified antennas have become popular in recent years for long-distance reception on bands where the long wavelength prohibits the practical use of parasitic beam antennas common at higher frequencies.
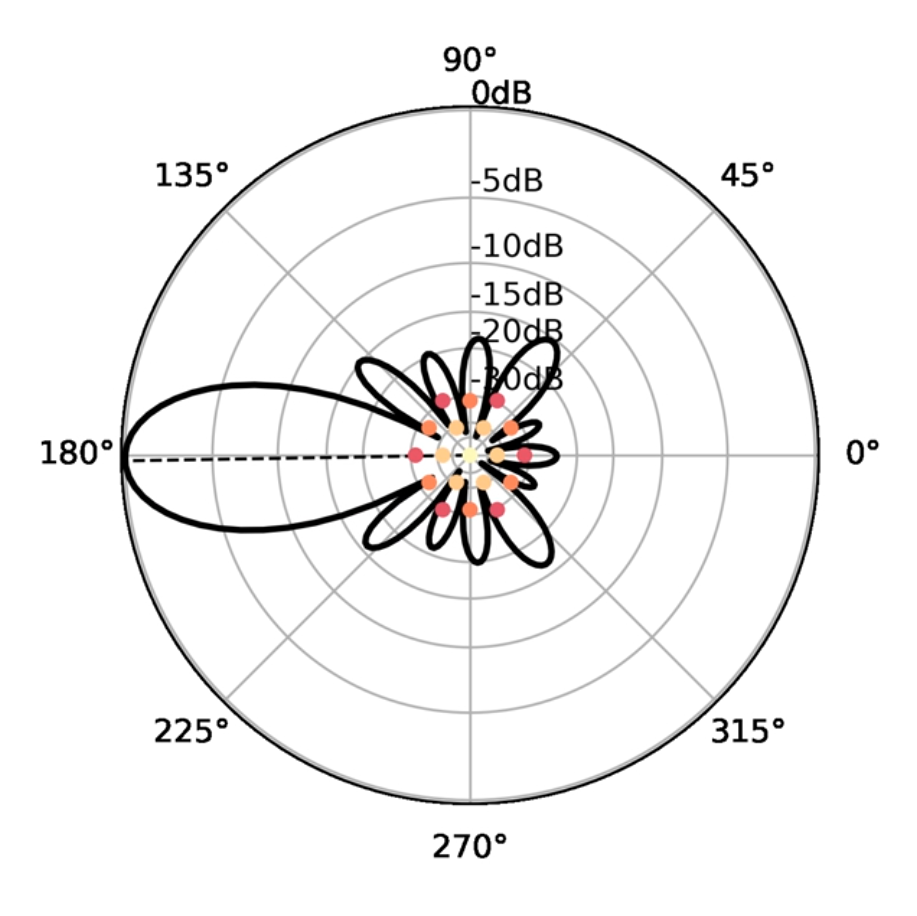
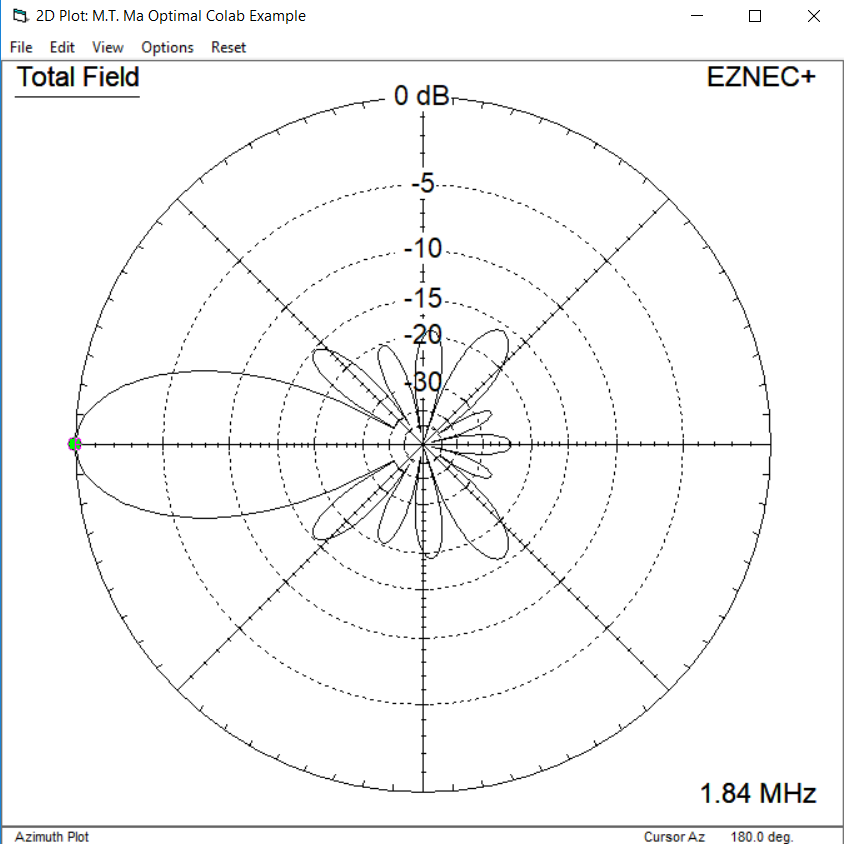
Array pattern from my notebook (left) and EZNEC NEC-2 simulation (right)
Inputs into the notebook include a list of arbitrary element coordinates in 2D as (x,y) tuples and an operating frequency. There are several options for generating regular element patterns at the beginning of the notebook. The pattern examples above use an unsual configuration on a hexagonal grid. This is not a typical array layout, but I wanted to highlight the ability of the technique for an arbitrary array geometry.
Results
The notebook uses Ma's algorithm to compute the optimal amplitudes and phases of the excitation currents of each element specified in the coordinate list. The algorithm involves the computation of a matrix involving integrals involving pairs of elements. The matrix can be calculated once. The optimal currents are quickly computed by multiplying the inverse of this matrix with a vector of complex phasors involving the desired elevation and azimuth angles for the main beam.
To visualize the results, I computed the optimal-directivity solutions of the array for many different azimuth angles, choosing the horizon as the optimal elevation angle as is typical for long-range ionospheric radio communications. The animation below plots the optimal pattern over the array shape. The relative element current amplitudes for each azimuth are visualized as the color of each element; darker colors are lower currents.
Azimuthal scan of optimal solutions for a regular hexagonal array
The desired azimuthal heading is visualized as a dashed line. Because of array symmetries, the optimal directivity pattern cannot always point precisely in the desired optimal direction, so you'll see the main beam of the array sweep back and forth to either side of the desired optimum direction as the beam scans around the compass.
The directivity of the hexagonal array as a function of azimuthal angle is shown below.
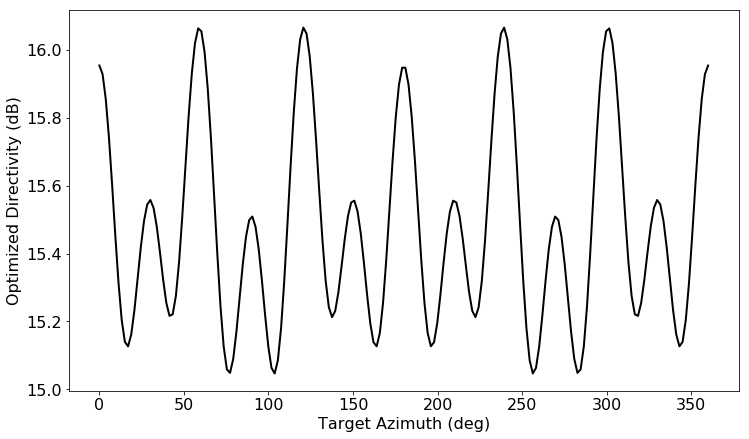
Optimal directivity of the hexagonal array
The notebook outputs text files to help import the element layouts and optimal currents into EZNEC, my NEC-2 finite-element antenna simulation software of choice. Here's a pre-built EZNEC model if you want to take a look at it:
EZNEC computes the effects of mutual coupling between antenna elements, and can be used to investigate whether the array can be made as a stable, realistic implementation. The low-frequency active antenna arrays used for receiving tend to swamp the element self-impedance with resistive loss to give a stable impedance and make mutual coupling negligible, so this is probably not too much of an issue. The Jupyter notebook also investigates the stability of the array pattern to random changes in excitation currents and amplitudes to help assess the stability of the array design against real-world imperfections in the phasing electronics.
Better Designs
I did the hexagonal array for fun, but its performance is not necessarily as good as other designs. Some of the best designs, inspired by more discussion in Ma's book, are concentric-ring arrays with staggered number of elements. The scan below is a 200 foot diameter array consisting of a five-element circle inside a nine-element circle. The pattern is much more stable as azimuth is varied.
Azimuthal scan for 200-foot diameter staggered-ring array
One more array, 7 elements inside 16 elements, 400 feet outer diameter.
Azimuthal scan for 200-foot diameter staggered-ring array
Since I've moved to Brooklyn, I don't build or test antennas anymore, so I haven't worked too much to develop practical, attractive designs with this tool. It is likely that like many exact optimization problems, many array designs will be too fragile to small phasing and amplitude imperfections to be realized in the real world. However, this notebook may still be a tool to investigate the best possible performance of different array layouts, and arrays with wider spacing and fewer elements should be fairly stable.
You should be able to open and run the notebook with modified array parameters using Google Colab. Drop me a note if you end up using this notebook to design and build an array for practical use. I'd love to hear about it.