Background
Large electromagnets provide an axisymmetric applied field to study magnetohydrodynamic phenomena in the UMD Three Meter Geodynamo Experiment in the absence of a self-excited dynamo field. The induced magnetic field reveals the structure and dynamics of the underlying flow, and when it's strong enough, Lorentz forces significantly modify the flow.
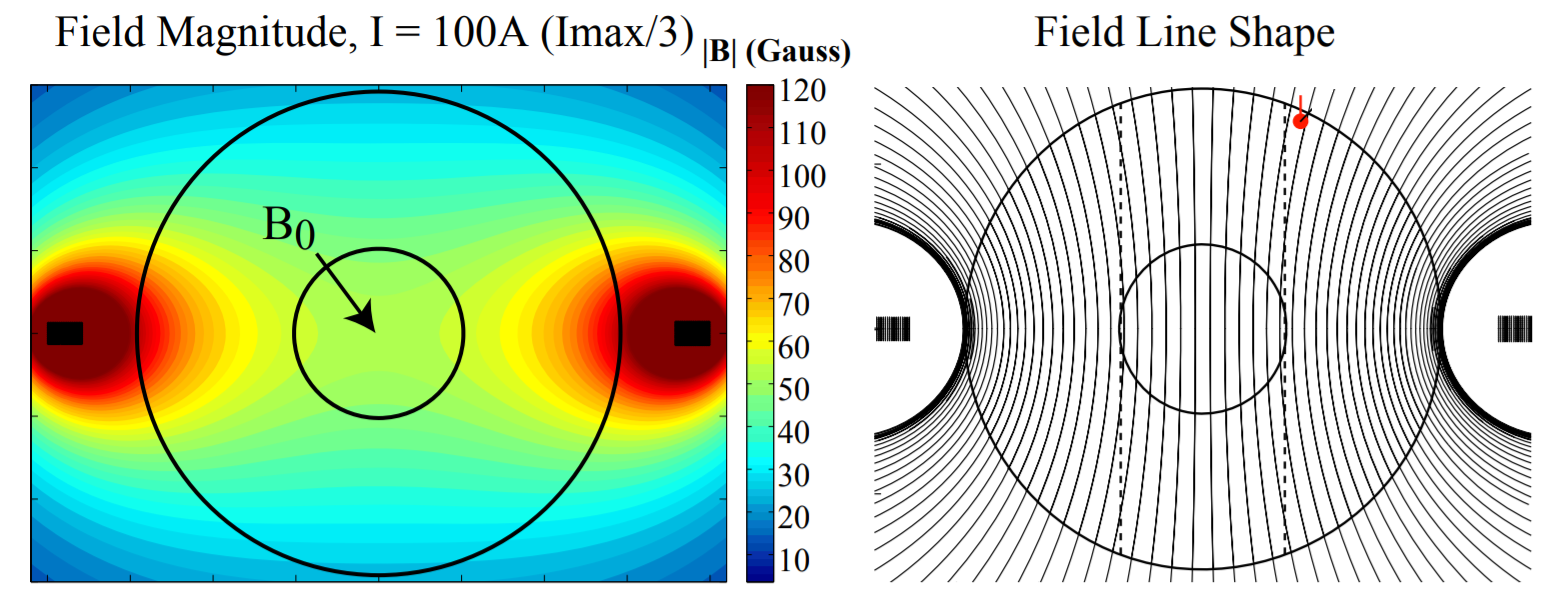
Applied field from a single equatorial magnet for the 3m experiment
Power Supply
Early MHD experiments used the single equatorial magnet pictured above. Later, two magnets were used in a Helmholtz pair for more uniform field throughout the liquid metal volume. Each of the two electromagnets is 160 turns of 1/2" square aluminum magnet wire wound into nearly 4m diameter coils. The coils handle up to 300A current, supplied by the Kinetics Industries three-phase rectifier supply pictured below.

80kW power supply, 0-270V, ~300A
The supply accepts a 4-20mA input for control, but the supply was shared between two labs and not physically located in either of them. It was used for heater control in the second lab and was sited in between the two spaces, in a mechanical room close to the 480V 3-phase panel. Therefore, it was most convenient to control it over the private wired network that connects the lab spaces. This prevented the need to switch analog control lines and prevented issues with wiring together two labs' acquisition hardware while still allowing easy control from either lab.
Controller
I designed the Arduino-based networked controller below using an Ethernet shield for communication and a Texas Instruments DAC8551 16 bit digital-to-analog converter to generate the analog control signal.

Digital-to-analog controller
Isolated power supplies and an optoisolator for the DAC's digital serial interface provide complete galvanic isolation between the Arduino and the supply's circuitry. The DAC's 0-5V output is amplified to 0-10V with an op amp and applied across the 470 ohm input resistance of the rectifier control input. Full scale and zero output are trimmed in firmware with a hard-coded calibration.
Current Sensing
Magnet current is measured using a Honeywell CSLA2DK non-contact Hall effect current sensor and one of the Arduino's built in 10 bit analog-to-digital converters. The supply output is fairly noisy, allowing the use of oversampling and decimation to increase the resolution of the current measurement.

Honeywell Hall-effect current sensor
A non-contact current sensor was chosen to maintain complete isolation between the high-power mains-connected circuitry and the Arduino controller.
Software
The controller uses a telnet interface. Simple text commands are used to set the supply voltage, to return a measurement of the current, and to shut down and reset the controller. The controller can be manually commanded from a terminal, but in normal operation, a graphical interface I wrote in Python establishes the telnet connection and allows easy control and display of the voltage and current. The GUI also logs the settings and measured current to a timestamped file for later data analysis.
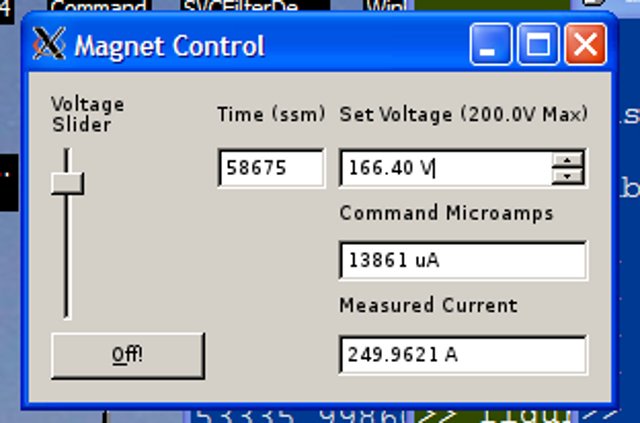
Python GUI software
The GUI is multithreaded to maintain a responsive user interface while handling logging and communication tasks that may block at times. You can view or get the code for the GUI and the Arduino firmware at GitHub:
Obviously, this is a fairly hazardous piece of equipment controlled using an insecure telnet protocol. I don't advocate this in general. No effort was expended to address network security or fault conditions for this project because:
- The supply and the controller are both completely powered down when not in use
- The controller is on a private internal network not bridged to the internet
- All possible DAC voltages result in safe operating conditions
- Standard operating procedure for magnet supply faults involves physically deactivating the supply